45度線モデルの「総需要」をグラフに書く【第3回】

45度線モデルを完成させる最後のピース。総需要の求め方について解説します。これを見た後は、自分で45度線が書けた上にどしてそうなるのか説明できるようになります。レポートや論述テストの参考にもしてくださいね。

45度線モデルのそもそもがわからない、と言う方や、総需要曲線以外の求め方についてはこちらの記事をご確認ください。

＞【第1回】45度線モデルのそもそも（意義や役割）

＞【第2回】45度線モデルの「軸」「45度線」の求め方

45度線の総需要曲線とは

45度線モデルの総需要曲線とは、一国の総需要のことです。

正確には、一国の総需要を「関数」化すると引けるグラフのことです。

一国の総需要は、国民の消費、民間企業の投資、政府支出、純輸出（輸出―輸入）から構成され（詳細は第1回の記事）、式で表すと

となります。

計算問題がよくでる

45度線は概念が理解できればOKなのですが、概念が理解できていることを試すために、大学の授業なのでは以下のような計算問題がよくでます。

専門用語が並べられて構えてしまいますが、ただ当てはめて足し算をすればよいだけです。

中学生レベルの算数しかやっていません。気軽に考えましょう。

「消費関数」（消費の仕組み）

総需要曲線　Yd=C+I+G+Ex-IMは、需要の種類をどーんと並べただけの単純な式です。

これだけだと、数学的には、グラフの傾きや切片がどうなるのかがわかりません。

実は、45度線モデルから考えても、需要の最も基本的な構成要素である「消費」の構造（仕組み）を細かく見ていくと、傾きや切片がわかり、グラフに描けるようになります。

45度線モデルの消費の構造（仕組み）

まず、消費は、一般的に次の構造になっています。

難しい言葉が使われていますが、そんなに複雑な話ではありません。

基礎消費

まず、基礎消費というのは、食費、家賃など、衣食住に必要な最低限の消費のことです。

所得が減ったからといって、まったく食糧を食べないことが不可能なように、基礎消費は可処分所得に関係なく消費額が決まります。

そのため、基礎消費は条件によって変化する（xやy等で表す）「変数」ではなく、常に一定の「定数」です。式を見ると、可処分所得とは独立しているので、それがわかります。

記号では、特に理由は無いですが「A」を使用しておきましょう（※ほかに、C0（シーゼロ）を使う場合も多いです）。

限界消費性向

限界消費性向とは、所得が1増えたときに、貯蓄ではなく消費に回す割合のことです。

例えば１万円拾ったときに、3000円貯金して、7000円を使ったらその人の限界消費性向は0.7となります（拾得したお金は交番に届けましょう）。

限界消費性向は1以下0以上の数で表します。数学的に書くと、0≦ｃ≦1　です。

なぜかというと、そうでないと成立しないからです。例えば限界消費性向が1.1ということは、拾った1万円の110％を使うことを意味します。存在しない10％があるのは意味不明ですよね。逆に0より少なくなると、「拾った1万円の-10％を使う」などともっと意味不明です。

限界消費性向は、だいたい小文字の「ｃ」が使われることが多いです。

可処分所得

「可処分所得」は可処分…つまり、使うことのできる所得と言う意味です。

といっても、例えば給料を30万円もらっても、税金で10万円引かれるなら可処分所得は20万円と言う意味でしかありません。

可処分所得はYで表します。

ケインズ型消費関数

以上を基に、消費を再定義すると、

となります。これを「ケインズ型消費関数」といいます。

「ケインズ」というのは、この関数を定義したのがケインズという経済学者だからです。

この式をさっきの総需要の式に当てはめます。

です。導き出されたこの式をグラフにしてみましょう。

グラフにする際の振り返り

導き出した総需要について、グラフにする前に、中学数学の超簡単な振り返りをします。ここでのグラフの書き方や関数は中学レベルでOKですが、計算問題ではないために意外と忘れている方も多いためです。そんなのわかっているよ、と言う方は次の項目まで飛ばしてください。

関数式（例：Y＝aX+b）をグラフにするには、次のような特徴がありますよね。

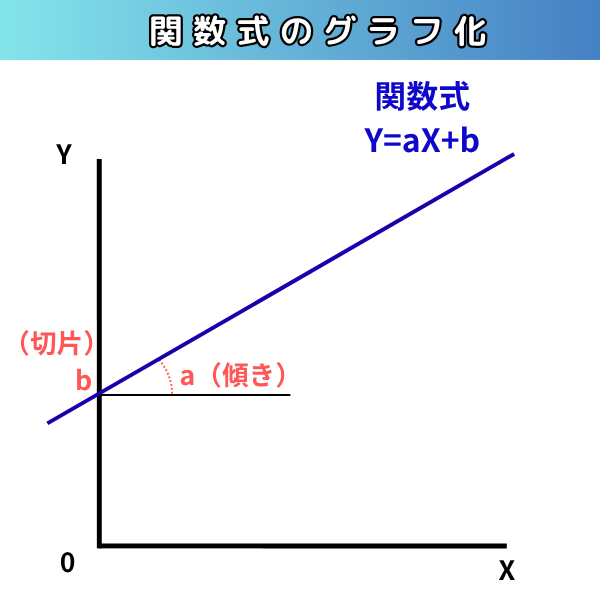
これ、もっと厳密に説明をつけ足すと、何を「傾き」にするかは、横軸にある記号がどれかによって変わります。

このグラフの場合、横軸に「X」とありますよね。だから、Xにくっついている「a」が傾きです。

そして、切片はbですが、この切片bは1文字だけである必要はありません。例えば、Y=aX+b+c+d+e+f+gとなっていれば、b+c+d+e+f+gが切片です。

この、関数やグラフの意味に関しては改めて詳しく紹介する記事を制作中です。

総需要曲線をグラフに描いてみる

総需要Ydは、

でした。これを元に、グラフを作図するために必要な、傾きと、切片を求めてみましょう。

傾きは？

さて、上記の式の中で、傾きはどれでしょうか？

45度線のグラフの横軸は「Y」ですね。ということは、このYについている記号が傾きです。Ydの式の中で、「Y」に貼り付いている記号は「ｃ」の限界消費性向です。

つまり45度線における総需要の傾きは限界消費性向（c）ということになります。

次に角度（まさしく「傾き」）を考えましょう。

ｃは「0≦ｃ≦1」という条件がありましたね。傾き「0」は横軸と平行な線で、傾き「1」は、45度線のことです。

なので、限界消費性向「c」の傾きは「平行以上、45度線以下」になります。

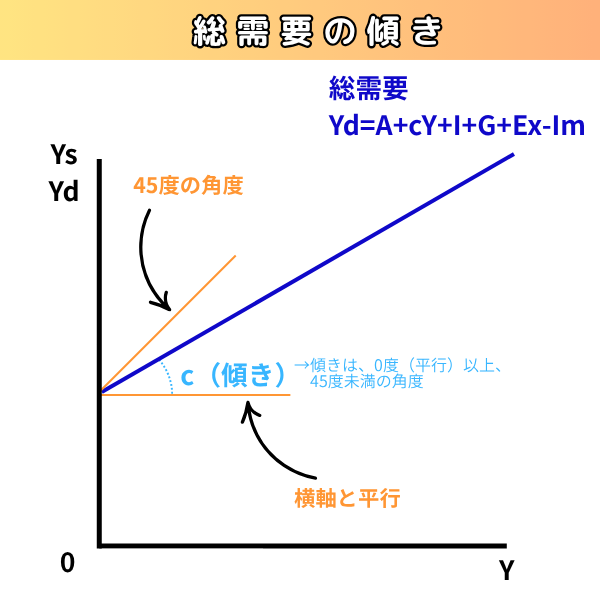
ん～傾きってこんな感じだったっけ？っとちょっと違和感を持ちましたか？

傾きは具体的な数字（1/2とか、1とか、3とか）が入る場合は、「横に2つ進んだら1つ上に行く（傾き1/2）」など、マス目を使って作図できます。しかし、今回は抽象的な「ｃ」なので、その特性がわかる形に作図できればOK、作図の際、45度を超えたりしなければ良いということです。

切片は？

では、切片はどれでしょう？

切片は、Y=aX+bのbに当たる部分ですが、「傾き以外の部分」が切片です。ということは、cY以外の「A+G+I+Ex-IM」が切片です。

これをグラフに書くとこうなります。

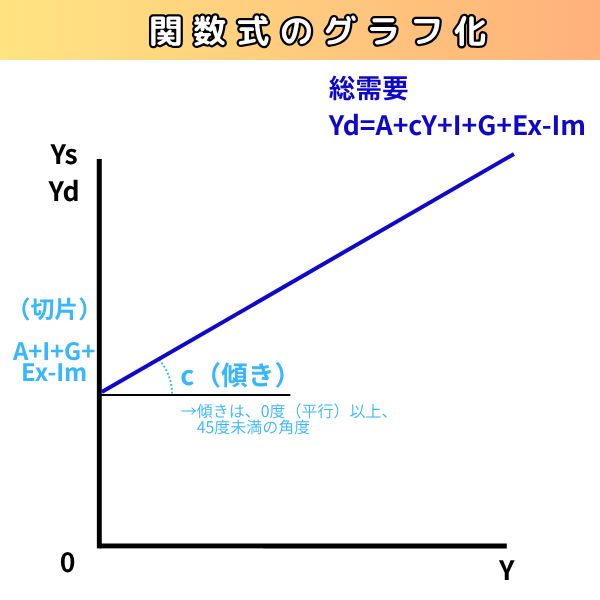
45度線に落とし込む

そしてこれをもとの45度線の引いてあるグラフに入れてみましょう。

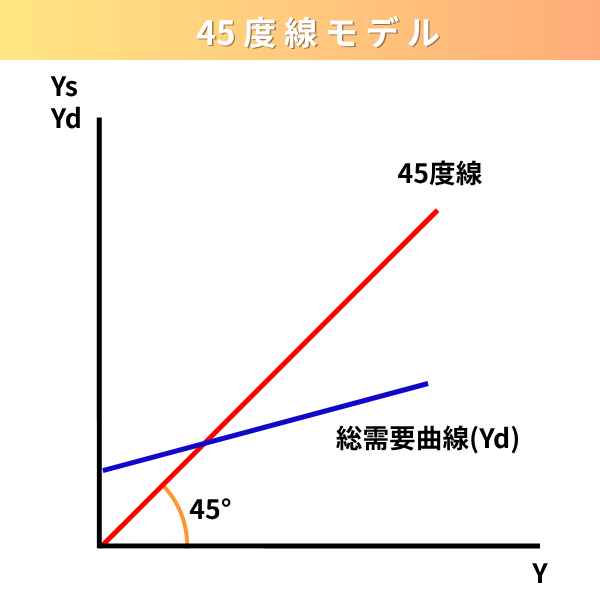
これで「45度線」の完成です。

実はここまでで、45度線の準備段階なのでした。実に３記事を要します。しかし、教科書や授業はこのあたりをすっ飛ばしてしまうために、わからない人にはわからないままに話が進んでしまします。

では、次の記事では、まさに45度線モデルの最大目的である「国民所得を求める」に進みます。